QuickBASIC programs

Analog Dial          ROCKET       GALCON    SUDOKU PROGRAMS

SUDOKU Solver Ver 8.6

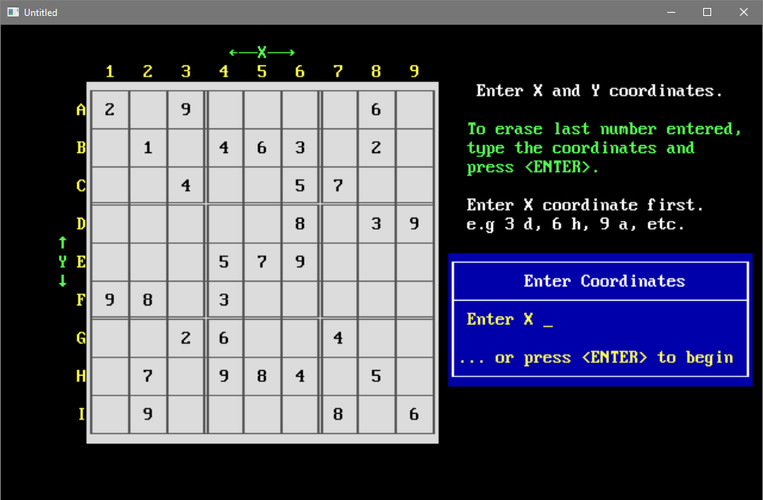
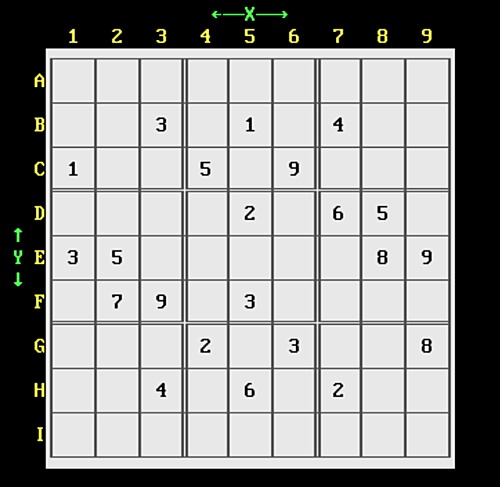
A typical SUDOKU board is divided into nine grids of nine cells. The object of the game is to fill in all the cells with a number from 1 to 9, without a double in any grid, row or column. This program attempts to do just that, even if it has to try it a million times!

SUDOKU solver screen after typing numbers in from a book.

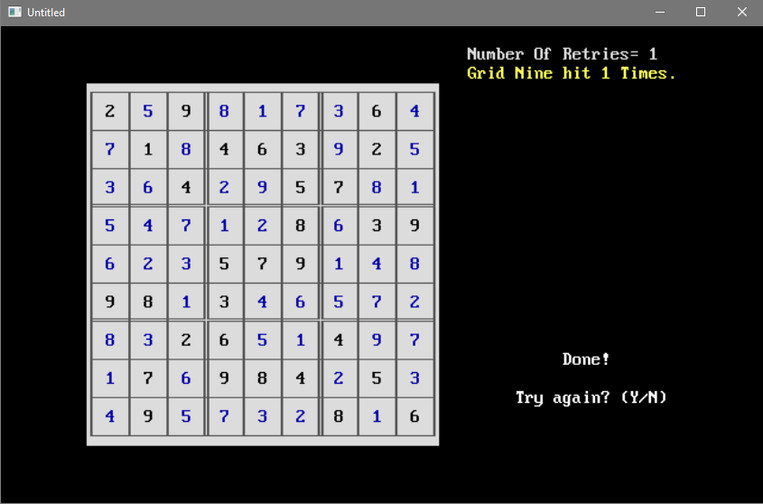
The solved puzzle.

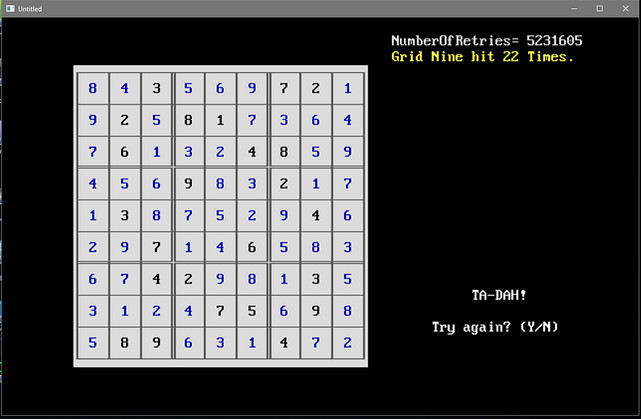
This early version of the program took over ten minutes and 5.2 MILLION attempts to solve this puzzle! The program was originally named "Pseudo Sudoku Solver."

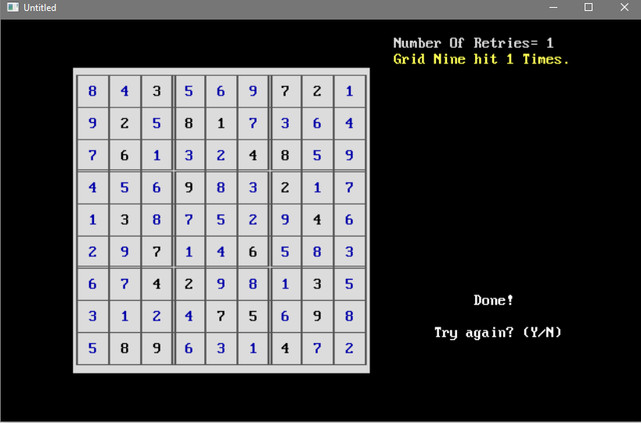
A later version solved it on a single pass.

How the program works

First, type in the numbers from an actual Sudoku puzzle. (You can type in random numbers, but you will occasionally create an invalid puzzle that has no solution.) After the last number is placed, press <ENTER> and the program will begin. The program has two main subroutines where the "puzzle solving" is done, named Board0  and Board1. Subroutines called  ViewGrid1 to ViewGrid9 are used by both to find numbers in the nine 3X3 grids. Board0 looks for cells that only have one solution, based on numbers populated in other cells. It goes through each empty cell, starting at the top-left, making a list of all possible numbers for each cell. It looks in the 3X3 grid that contains the cell, then across the row and up and down the column. If the list has a single digit on it, it puts it in the cell. If the list contains more than one digit, it ignores the list and goes to the next cell. Each number that it finds increases the chances it will find another number. It scans the puzzle until no more numbers are found, then exits. If it's an "easy" puzzle, it will sometimes solve the puzzle during this phase, but don't count on it. 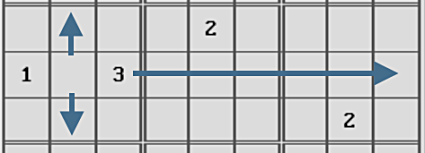  Flaw in the program logic It's obvious that the only digit that can go in the left-center cell is a "2." However, the program doesn't see it. It only "looks" in the direction of the arrows, blind to the other 2s. That's OK, it will eventually find it. Board1 then starts in the top-left cell. It finds the first available empty cell. It generates a random number, and looks within the 3X3 grid for any numbers already there. If there is a number in the grid that matches the random number it just generated, it generates a new number. If a matching number is not found in the 3X3 grid, it looks left and right, and up and down. If a matching number is found, it generates a new random number. If a matching number is NOT found, it puts the number in the cell. If no number can be put into the cell, it erases all the numbers in the 3X3 grid and starts over. The process repeats till all 81 cells contain a number. The exception is the last cell in each grid. Since eight digits have already been used, there is only one digit that can possibly go into the space. If it can't be used, the grid is erased and reprocessed.               This image shows how the "Board1" subroutine works. 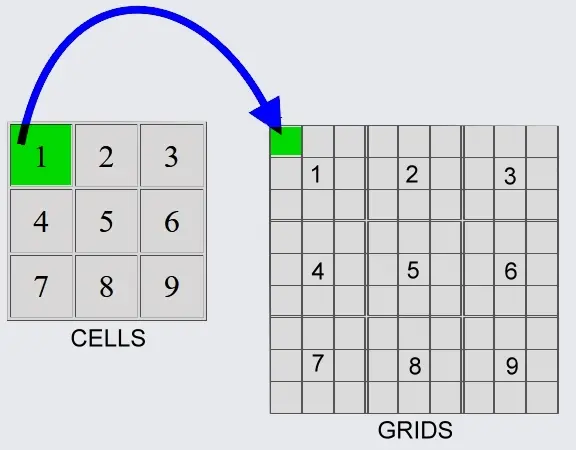In this case, it has randomly selected the digit "5."           Both the cells and the grids are processed in the order below, from 1 to 9. Changing the order does not seem to have an advantage. Starting in grid 5 is counterproductive. I don't know why.       When a grid is filled, the next grid is begun starting at the top-left cell. If a number can't be entered into a cell after 20 attempts, the grid will start over. If the grid has restarted 20 times and still can't be completed, the whole board starts over. Why 20 times to enter a number? You may well ask! The numbers are generated randomly. If you generate random numbers between 1 and 9 you're going to get some doubles before you get every digit. I analyzed the minimum number of attempts needed to generate every digit from 1 to 9, and it seems to be about 20, though occasionally a number will be missed. (I initially had it set to 40.) For example, If you generate 20 random digits from 1 to 9 you get something like this: 5 4 7 4 8 6 6 9 5 2 9 1 3 5 8 9 5 3 1 8 - all numbers from 1 to 9 are present - barely. There is only a single "2" but "5" appears four times. (These were actually generated by the Sudoku program.) As soon as a number can be placed in a cell the program goes on to the next cell, so why place a limit on the number of random digits? Because if a number can't be placed, it will keep trying the same nine digits forever. So in this case, 20 times is the limit. Originally, the program wasted time trying numbers it already attempted, such as trying the number "5" four times. Starting in Version 7.2 the program "remembers" numbers it has already used. If a grid or the entire board starts over, the numbers that the user has entered or that Board0 has found are put back in their cells by a subroutine named ReloadData. The program is not able to "see" the whole board at once, like a human can. It only sees the 3X3 grid of the cell it is currently working in, as well as the row and column. It keeps plugging numbers in over and over till the puzzle is complete. Each cell has it's own programming. You can think of it as 81 sub-routines. I programmed the first cell for Board1, then copied, pasted and edited it 80 more times. I did the same thing for Board0. It was a bug factory. A single mistake would produce 80 more bugs! Once the bugs were out the program worked very well, though it can still take quite a while to solve a "hard" puzzle. And I mean QUITE a while. It has "AI" or "artificial ignorance." The challenge was figuring out how to tell the computer to solve the puzzle, since I'm actually not very good at Sudoku. Even before I started, there were some basic questions, such as, "How does the program know it's done?" I thought that one way was to check and see if every row and column added up to 45. In the end, it wasn't necessary. When the bottom-right cell is filled, there is nothing left for it to do. When I say that the programs "looks" at a cell and "sees" a number I mean it almost literally. The program is displayed on an  80 x 25 text screen. It queries the screen coordinates and returns the number found there. For example, it will look 40 columns across and 15 rows down and get the number in that spot on the screen. So here's a question to keep you awake tonight: Will the program work if the monitor is turned off?

DOWNLOAD

Click on icon above to view or download the source code   Click on icon above to download SUDOKU86.exe

Note: Browsers don't like .EXE files.  Please rename "SUDOKU86.RenameToExe" to "SUDOKU85.exe" after downloading.

According to a Wikipedia article titled "The Mathematics of Sudoku," there are 6,670,903,752,021,072,936,960 ways to fill in a blank Sudoku board. This explains how the program can fill in a blank board so quickly. You would think that the number is just a factorial of 81 (81 x 80 x 79 x 78 x 77....etc). However, the factorial of 81 is 5,797,126,020,747,367,985,879,734,231,578,109,105,412,357,244,731,625,958,745,865,049, 716,390,179, 693,892,056,256,184,534,249,745,940,480,000,000,000,000,000,000. The difference in the numbers is that the factorial of 81 doesn't follow any Sudoku rules. An actual Sudoku puzzle will have just one solution. The minimum number of clues to complete a puzzle is 17.

Here is a very interesting Sudoku puzzle. It's the number Pi in order, which is 3.141592653589793238462. This puzzle was  created by Phillip Newman in March of 2021. The "Sudoku Solver" program solved it in 221,385 attempts. I ran it a second time and it took 555,242 attempts, and a third time it only took 6349 attempts. The program really struggles with this, but it will eventually solve it. Since it's random, the only question is, will it solve it sooner rather than later? It was interesting to see that Board0 found three numbers before Board1 even started working. I found the puzzle here.

Last updated July 2022

NEXT