|
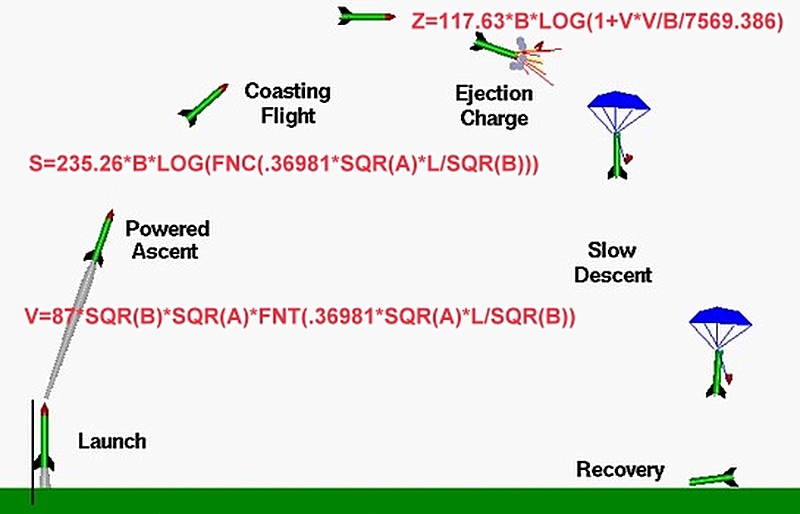
ROCKET is a model rocket
altitude prediction program written by Michael Gasperi in
the 1980s and sold by Estes Industries. The program, which runs in BASIC,
is called "PC ASTROCAD." The Mike Gasperi version
is "bare bones," so my brother-in-law Andy and I began to write a full featured
program around Mike's calculations. It would
include graphics, color, menus, a database of engines, and a
way for the user to add engines and save rocket
specifications.
We started this in the 1980s. At that point in time the IBM
XT was being sold, but it cost a bazillion dollars. As far
as we were concerned it was only a picture in some computer
magazine. Andy was using a Radio Shack Color
Computer II and I used a Mattel Aquarius.
This resulted in slightly different code.
The
version of BASIC used by the Aquarius didn't have the "DEF
FN" (DEFine FuNction) statement, nor did it have the
ATN (arctangent) function. Both were used in the
original Estes calculations. At first I was very
disappointed that I couldn't run the program (and Andy
could!), but then I resolved to take the calculations apart
so they would work on the Aquarius.
The Aquarius version can be found at the bottom of this
page.
| |
|
|
|
|
| |
Mattel
Aquarius |
|
Tandy Color
Computer II |
|
|
This was in the early days of home computing, when the
computer monitor was your TV set and programs were stored on
cassette tape. When DOS based computers became available
that would all change, but they were (in the beginning) too
expensive to actually own one. Then one fateful Christmas Day, Andy found a
Tandy TL, which ran on MS-DOS, under the
Christmas tree! I built an XT clone, then an AT clone, then a 386,
486, Pentium, etc, and so did Andy. Back then you didn't have to pay for an
operating system. Of course, you were "supposed" to pay for
it, but we never did.
We retyped the program into the new computers, since they
were incompatible with the cassette tapes from our older
machines. As time went on we used BASIC, BASICA and GW-BASIC
(Microsoft improved MS BASIC when improved versions of
MS-DOS were released).
In 1988 QuickBASIC ver 4.5 was released. We moved the
program to QuickBASIC and would share our new versions of
ROCKET back and forth via floppy disk, since we worked on
them independently. I would take Andy's improvements and
copy them into my version and Andy did the same with mine,
though not all the "improvements" made it into each other's
versions.
The program began in two color "high
resolution" CGA (SCREEN 2 in BASIC). When
EGA and VGA became available we changed it to run in EGA, but it
would still run in CGA if it had to. The program would check
for EGA and drop to CGA if an error was detected. You couldn't toggle it manually.
(The CGA code has since been deleted.)
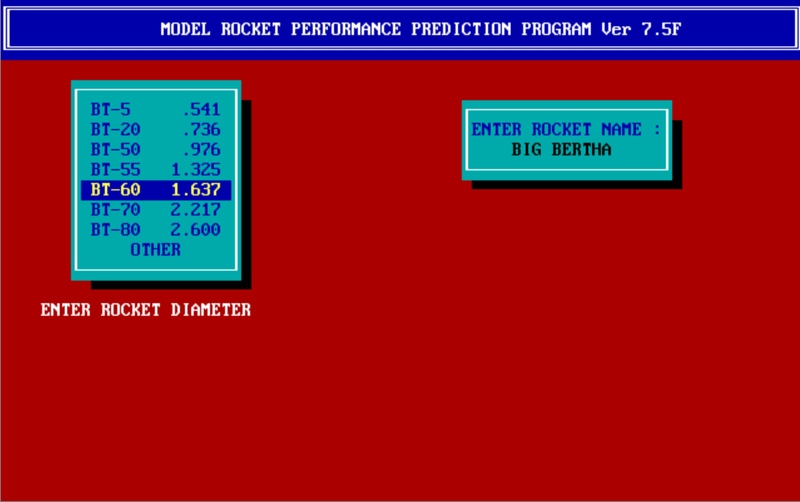
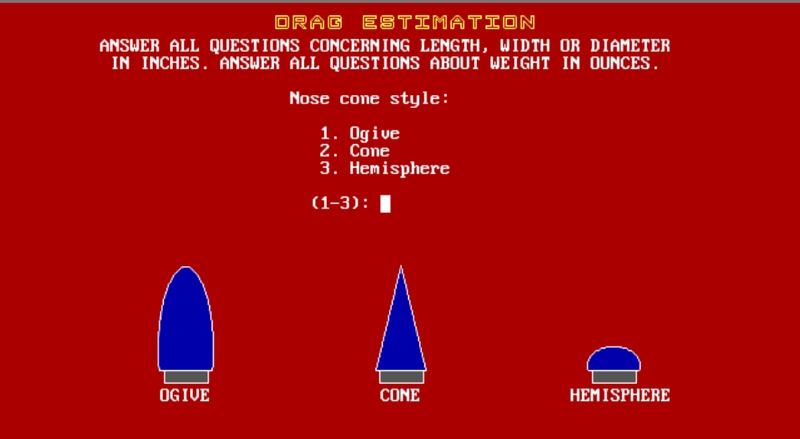
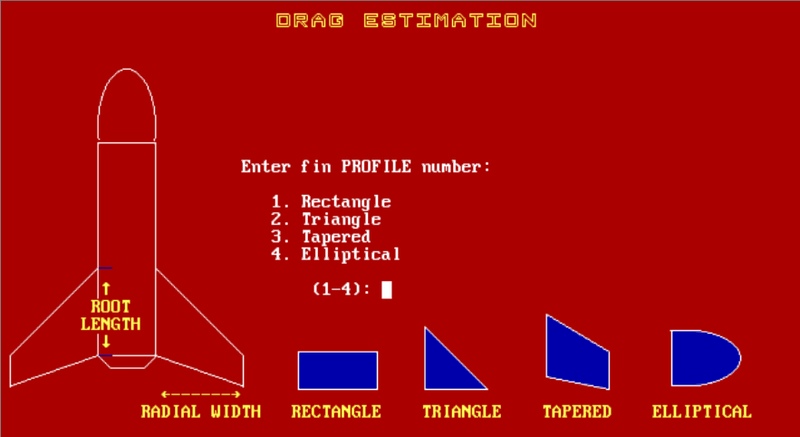
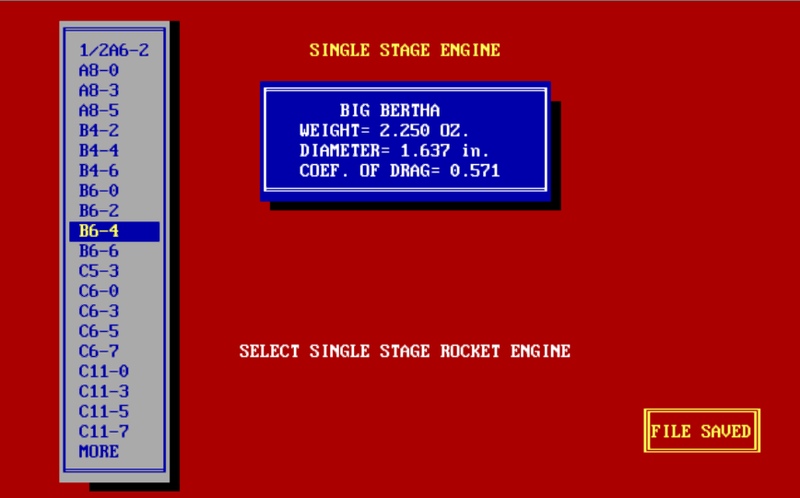
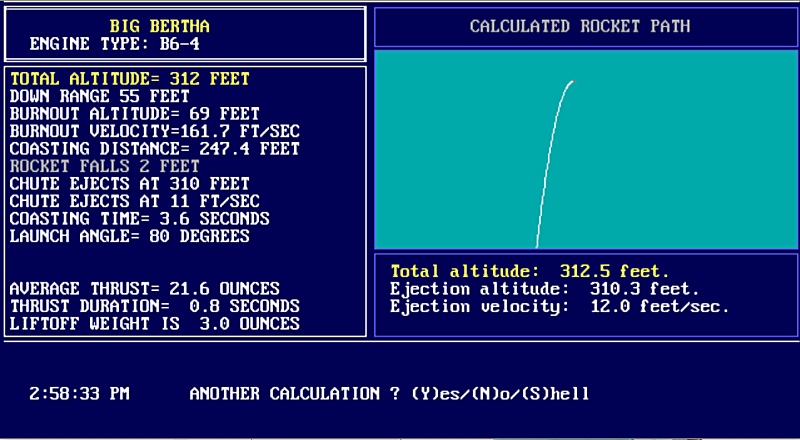
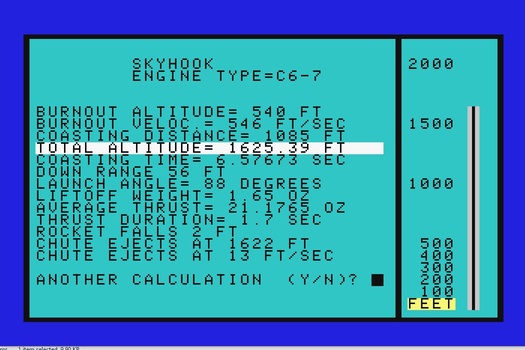
Below are some screen caps of the program. It's easy to
use. Once you define a rocket you can save the specs to a file and
then run the program using various engines to determine the
best one.
|